На засіданні Бюро Відділення фізики і астрономії НАН України 23 лютого 2021 року молода вчена, докторантка відділу комп’ютерного моделювання багаточастинкових систем Інституту фізики конденсованих систем НАН України кандидат фізико-математичних наук Христина Гайдуківська розповіла про отримані в інституті нові результати у галузі фізики полімерів. Доповідь зосереджувалася на впливі особливостей просторової структури на універсальні властивості макромолекул у розчинах.
 Лауреати Премії Президента України для молодих вчених – співробітники Інституту фізики конденсованих систем НАН України (зліва направо):доктор фізико-математичних наук Максим Дудка (2009), кандидат фізико-математичних наук Христина Гайдуківська (2017) та доктор фізико-математичних наук Вікторія Блавацька (2009) |
Полімери – це молекулярні структури, які складаються з великої кількості повторюваних ланок (мономерів) однакового чи різного хімічного складу. Один із типових представник таких структур – молекула ДНК, що може містити десятки тисяч складових блоків (нуклеотидів), а також білки, які є основою живих організмів. Матеріали, синтезовані на основі полімерних макромолекул, широко використовуються в техніці та медицині. Такі макромолекули у розчинах часто формують довгі гнучкі ниткоподібні ланцюжки (див. рис.1), які за певних умов можуть утворювати зв’язки між собою, формуючи галужені та складногалужені структури, прикладом чого є деякі модифікації крохмалю.
 Рис.1.Схематичне зображення полімерного ланцюжка із 1500 «мономерів» у хорошому розчиннику |
Найпростіший представник класу галужених полімерів – зірковий полімер, який складається з певної кількості лінійних ланцюжків – гілок, з’єднаних спільним центром галуження. Розчини таких молекул використовуються як модифікатори в’язкості в мастилах і фарбах, пропонуються для використання у пластиках для 3D-друку, виступають як структурні елементи полімерних мереж і міцел. Як цікаві та багатообіцяючі, з огляду на перспективи їхніх технологічних застосувань, розглядаються макромолекули з більш ніж одним центром галуження, так звані розеткові та пом-пом-структури (див. рис.2).
 Рис.2. Схематичне зображення складногалужених полімерів. Тут лініями позначено полімерні ланцюжки. Структуру з одним центром галуження називають розетковим полімером, а з двома – пом-пом-полімером |
Теоретичне вивчення подібних макромолекул потребує розроблення спеціального математичного апарату для їх опису. Водночас, статистичний опис таких об’єктів дає змогу виокремити низку цікавих і важливих характеристик макромолекул, які не залежать від деталей хімічної структури, а лише від їх архітектури (ступеня галуженості), середовища чи агрегатного стану, в якому вони перебувають. Такі властивості називають універсальними. Їх можна досліджувати, використовуючи методи чисельного моделювання або ж аналітичні підходи на основі математичних моделей із невеликою кількістю параметрів. Обидва напрями досліджень традиційно розвиваються і застосовуються в Інституті фізики конденсованих систем НАН України.
До вищезгаданих універсальних величин належать, зокрема, характеристики розміру та форми макромолекул у розчині. Наприклад, радіус гірації, що визначає середню відстань мономера від центру мас макромолекули і характеризує ефективний розмір молекули в розчині, зростає зі зростанням маси макромолекул за степеневим законом із універсальним показником, який залежить лише від вимірності простору та якості розчинника. Цей показник буде найменшим у поганому розчиннику, коли макромолекула згортається в тісну глобулу з якнайменшою поверхнею контакту з розчинником, та найбільшим – у випадку так званого хорошого розчинника. Цікаво й те, що цей показник однаковий для лінійних і галужених полімерів. Розраховуючи його, використовують порівняно прості моделі, що враховують лише зв’язність мономерів.
Останніми роками дослідники Інституту фізики конденсованих систем НАН України зосередили основну увагу на вивченні складних полімерів, які характеризуються різноманітністю хімічної будови (різні частини макромолекули – так званого кополімера – по-різному взаємодіють із розчинником) і топології (полімерні ланцюжки, які формують макромолекулу, з’єднуються в центрах галуження та можуть утворювати петлі, на рис.2 схематично зображено випадки з одним і двома центрами галуження).
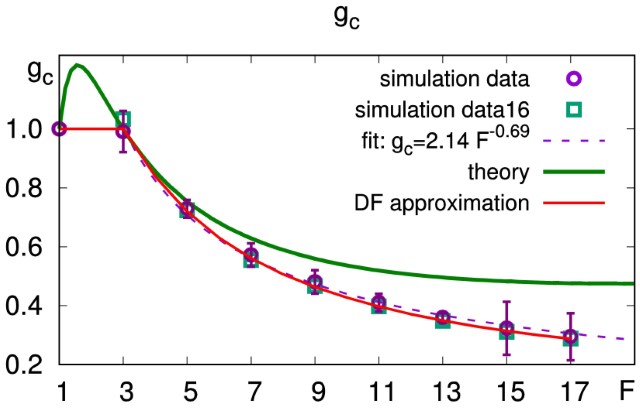 Рис.3. Відношення радіусу гірації пом-пом-полімера до радіусу гірації лінійного ланцюжка. Суцільними лініями зображено результати аналітичного опису, а символами – чисельного моделювання |
У такий спосіб вивчено універсальні властивості складних полімерних макромолекул із різною структурою. До прикладу, розмірне співвідношення g (зображене на рис.3) вказує, наскільки пом-пом-полімер (структура з двома центрами галуження на рис.2) є компактнішим за лінійну макромолекулу такої ж молекулярної маси. Що компактніша макромолекула, то ближче до сфери перебуває у розчині її форма – макромолекули з одним центром галуження більш сферичні, ніж макромолекули з двома центрами, а форма лінійної макромолекули видовженіша. У практичних застосуваннях це, зокрема, позначається на меншій в’язкості полімерних розчинів, що містять галужені макромолекули, порівняно з розчинами лінійних полімерів, якщо такі молекули мають однакову масу, складаються з однакових мономерів і перебувають у тому ж розчиннику.
Отримані результати важливі не лише для пояснення експериментальних спостережень, а й корисні для розуміння таких явищ, як згортання ДНК і протеїнів чи зміна в’язкості макромолекулярних систем, що суттєво при виробництві ліків.
* * *
Результати згаданих досліджень опубліковано у таких статтях:
V. Blavatska, K. Haydukivska and Yu. Holovatch. Shape analysis of random polymer networks, J. Phys.: Condens. Matter, 2020, vol. 32 p.335102 (1-11)
https://doi.org/10.1088/1361-648X/ab88f4
K. Haydukivska, V. Blavatska, J. Paturej, Universal size ratios of Gaussian polymers with complex architecture: radius of gyration vs hydrodynamic radius, Scientific Reports. 2020. Vol.10. No. 1. P. 14127
https://doi.org/10.1038/s41598-020-70649-z
K. Haydukivska, O. Kalyuzhnyi, V. Blavatska, and J. Ilnytskyi, On the swelling properties of pom-pom polymers in dilute solutions. Part 1: symmetric case, Journal of Molecular Liquids. 2021. Vol. 328. P.115456
https://doi.org/10.1016/j.molliq.2021.115456
За інформацією Інституту фізики конденсованих систем НАН України