Звітній період був відзначений подальшим розвитком наукових досліджень, посиленням наукових зв’язків з провідними закордонними науковими центрами, активною участю в міжнародних проектах, в т.ч. в програмі HORIZON 2020, розширенням взаємодії наших установ з іншими установами Академії та вищими навчальними закладами, а також з крупними підприємствами України, зокрема, з Державним підприємством «Конструкторське бюро «Південне» «ім. М. К. Янгеля», ПАТ «Укртрансгаз» та ін. Перед тим, як перейти до огляду отриманих результатів, нагадаю, що до складу Відділення входять Інститут математики, Інститут прикладної математики і механіки, Інститут прикладних проблем механіки і математики
ім. Я. С. Підстригача, його Центр математичного моделювання, Математичне відділення Фізико-технічного інституту низьких температур ім. Б.І. Вєркіна. Стосовно останнього Відділення здійснює тільки науково-методичне керівництво. Працювали дві Наукові ради: Обчислювальна математика та Математичні проблеми механіки (слайд 1).

Слайд 1

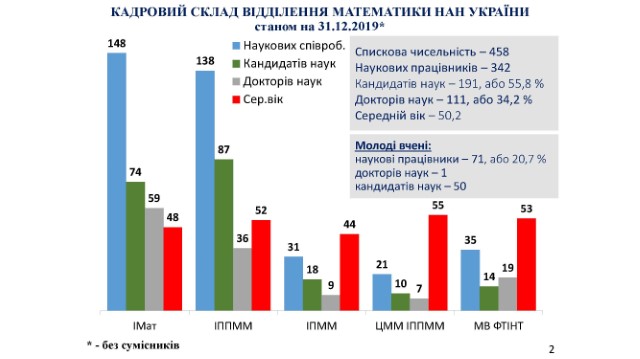
Станом на 31.12.2019 до складу Відділення входило 12 дійсних членів (академіків) та 17 членів-кореспондентів НАН України, загальна чисельність наукових працівників становила 342 особи, з них 111 докторів та 191 кандидатів наук (слайд 2).

Слайд 2

До основних напрямів наукових досліджень Відділення математики належать: диференціальні, функціонально-диференціальні рівняння, динамічні системи та нелінійні граничні задачі для рівнянь з частинними похідними; функціональний та нелінійний аналіз, теорія функцій дійсної та комплексної змінних; стохастичні диференціальні рівняння, теорія випадкових процесів та фрактальний аналіз; алгебраїчні, геометричні та топологічні структури; математичні проблеми динаміки, стійкості та керування руху складних механічних систем; математичне моделювання природних і технологічних процесів; обчислювальна математика; математична фізика і математичні методи статистичної фізики (слайд 3).

Слайд 3

Щороку на засіданнях Бюро Відділення розглядалися звіти про підсумки наукової, науково-організаційної та господарської діяльності підпорядкованих установ, питання підвищення ефективності та оптимізації їх роботи, здійснювалася оцінка отриманих результатів, роботи аспірантури і докторантури, стан поповнення молоддю і підготовки наукових кадрів вищої кваліфікації, заслуховувалися наукові доповіді з актуальних наукових напрямів та наукові повідомлення молодих вчених. На звітних сесіях Загальних зборів Відділення визначалися подальші перспективи розвитку фундаментальних та прикладних досліджень в установах Відділення з метою визначення основних наукових напрямів та найважливіших проблем фундаментальних досліджень у галузі природничих, технічних і гуманітарних наук. Велику увагу приділено реалізації Концепції розвитку НАН України на 2014-2023 рр.

До результатів світового рівня, які опубліковані у найбільш авторитетних у світі виданнях можна віднести наступні.

В Інституті математики досліджено параболічне рівняння, яке описує феноменологічну модель безгазового горіння на циліндричній поверхні, вивчено питання існування та стійкості біжучих хвиль, а також характер набуття та втрати їх стійкості. Такі задачі виникають, наприклад, при дослідженні процесів горіння гетерогенних та конденсованих систем та в теорії нестаціонарного горіння твердого ракетного палива (акад. НАН України А.М. Самойленко).

Розроблено загальну концепцію дослідження нелінійних крайових задач для диференціальних систем із запізненням, рівнянь з імпульсною дією,
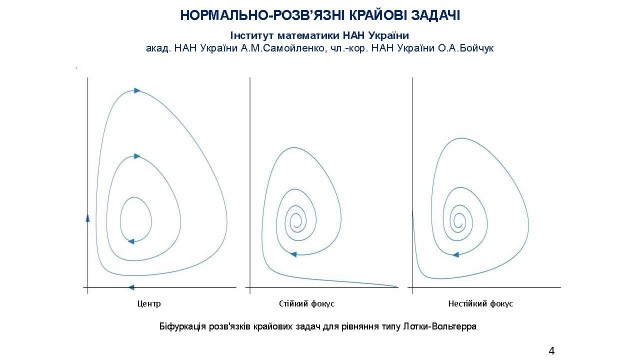
інтегро-диференціальних рівнянь, нормально-розв’язних та узагальнено- нормально-розв’язних операторних рівнянь у банахових та гільбертових просторах. Такий підхід дозволяє досліджувати як недовизначені, так і перевизначені резонансні задачі, що виникають при моделюванні реальних прикладних процесів у фізиці, хімії та інших галузях науки. Наприклад, при вивченні динаміки популяцій у численних задачах біології досліджуються системи типу Лотки-Вольтерра, а саме – біфуркація їх розв’язків (акад. НАН України А.М.Самойленко, чл.-кор. НАН України О.А.Бойчук) (слайд 4).

Слайд 4

Розроблено ефективний чисельний метод розв’язування зворотньої у часі задачі для параболічного диференціального рівняння першого порядку з необмеженим операторним коефіцієнтом у банаховому просторі. Метод базується на регуляризації вихідної задачі за допомогою двоточкової нелокальної умови та допускає трирівневе розпаралелювання обчислень й може бути застосований для оптимізації обчислень у фінансовій математиці, цифровій обробці зображень, гідрології тощо (акад. НАН України В.Л.Макаров, В.Б.Василик, Д.О.Ситник).

Проведено класифікацію рівнянь Шредінгера зі змінним параметром маси, які є іваріантними відносно групи обертань та допускають додаткові інтеграли руху, описано алгоритм їх інтегрування та показано, що усі вони є суперінтегровними і точно розв’язними (чл.-кор. НАН України А.Г. Нікітін).

Розроблено техніку обчислення модулів Коена-Маколея над неізольованими поверхневими особливостями. За її допомогою побудовано широкий клас неізольованих поверхневих особливостей ручного типу, а також контрприклад до відомої проблеми Шрайєра про особливості дискретного
Коен-Маколієвого типу (чл.-кор. НАН України Ю.А. Дрозд, І.І. Бурбан).

Побудовано уточнену математичну модель статистичної динаміки нескінченних систем часток із взаємодією, в якій враховується пам'ять системи, що є актуальним для такого розділу загальної екології, як популяційна екологія. Це дозволить створювати алгоритми дослідження конкретних задач, що описують динаміку зміни чисельності певних видів тварин, рослин, мікроорганізмів та їх взаємодії у різних умовах навколишнього середовища. Для цього в диференціальні рівняння системи вводяться диференціально-згорткові оператори типу дробових похідних за часом. Для таких моделей доведено властивість уривчастості, що характеризує хаотичну поведінку
системи (чл.-кор. НАН України А.Н. Кочубей, Ю.Г. Кондратьєв).

На основі якісного аналізу режимів колективної поведінки зв’язаних фазових осциляторів введено математичне поняття “химерного стану”, яке відповідає фізичному явищу колективної динаміки у складних осциляційних системах, що дозволило дослідити колективну динаміку та біфуркацій у осциляторних мережах різної архітектури, побудувати мінімальні осциляторні мережі, що мають стійкі “слабкі химери”, та модульні системи із гетероклінічними та хаотичними химерами. Дослiдження явищ колективної динамiки може бути застосоване в описi взаємодiї найпростiших частинок, масивiв з’єднань Джозефсона, електрохiмiчних осциляторiв, масивiв лазерiв, нейронних мереж та взаємодiї живих органiзмiв (О.А. Бурилко) (слайд 5).

Слайд 5

В Інституті прикладної математики і механіки отримано теореми існування розв’язків задачі Діріхле для напівлінійних рівнянь дивергентного виду з вимірними коефіцієнтами при неперервних крайових умовах в довільних областях з невиродженими граничними компонентами. Дано застосування до математичних моделей теорії горіння, стану плазми і процесів дифузії та абсорбції при хімічних реакціях в анізотропних та неоднорідних середовищах (чл.-кор. НАН України В.Я. Гутлянський, В.І. Рязанов, О.В. Нєсмєлова).

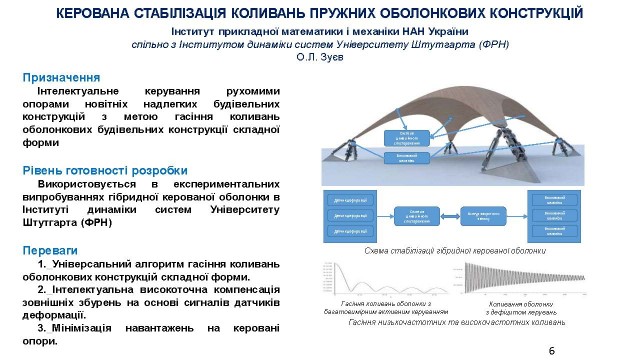
В рамках спільних досліджень з Інститутом динаміки складних технічних систем ім. Макса Планка (Німеччина) розроблено чисельно-аналітичний підхід до математичного моделювання, оптимізації напружень та гасіння коливань керованих пружних оболонкових конструкцій зі складною геометрією. Отриманий результат призначений для інтелектуального керування рухомими опорами новітніх надлегких будівельних конструкцій з метою гасіння коливань оболонкових будівельних конструкції складної форми завдяки універсальному алгоритму гасіння коливань таких конструкцій та інтелектуальній високоточній компенсації зовнішніх збурень на основі сигналів датчиків деформації та мінімізації навантажень на керовані опори (О.Л. Зуєв) (слайд 6).

Слайд 6

Виявлено новий клас функцій керування для задач динамічної оптимізації, який з теоретичної точки зору узагальнює низку існуючих алгоритмів пошуку екстремуму та дозволяє будувати нові керування, а з практичної точки зору дозволяє синтезувати керуючі алгоритми з потрібними властивостями, які відповідають різноманітним вимогам практики. Серед таких властивостей: підвищення точності алгоритмів та зменшення амплітуди коливань; простота впровадження; зменшення часу, необхідного для реалізації поставленої мети; обмежене споживання обчислювальних потужностей тощо. Отримані результати відкривають нові перспективи щодо оптимізації складних динамічних та багатоагентних систем, зокрема, систем комп’ютерного керування рухом програмованих мобільних роботів (В.В. Грушковська) (слайд 7).

Слайд 7

В Інституті прикладних проблем механіки і математики ім. Я.С. Підстригача на основі нових підходів до розв’язування рівнянь Максвелла і Матіссона, які описують поширення полів і рух частинок в околах чорних дір Шварцшільла і Керра, вперше в світі виявлено і точно описано ефекти впливу обертання чорної діри Керра на поляризацію і закрученість електромагнітного випромінювання та описано рух швидких спінових частинок навколо чорної діри Шварцшільда. Передбачені ефекти можуть стати предметом спостережень з метою перевірки загальної теорії відносності та встановлення параметрів чорних дір (В.О. Пелих, Р.М. Пляцко, Ю.В. Тайстра, М.Т.Феник) (слайд 8).

Слайд 8

Побудовано розв'язок квазістатичної задачі термопружності для кусково-однорідної структури, складеної із термочутливих контактуючих півпростору та шару за конвективного теплообміну з середовищем сталої температури. Відповідну задачу теплопровідності, лінеаризовану за допомогою перетворення Кірхгофа та методу лінеаризувальних параметрів, розв’язано за допомогою інтегрального перетворення Лапласа з використанням регуляризованої формули Пруднікова для його числового обернення. Для вказаної структури визначено та досліджено термопружний стан, необхідність урахування якого виникає при оцінюванні міцності змодельованого нею теплонавантаженого елемента конструкції (акад. НАН України Р.М. Кушнір, О.М. Вовк, Т.Я. Соляр).

Розвинуто теорію стовпцево-рядкових некомутативних визначників, у якій запропоновано прямі методи, а саме, аналоги правила Крамера знаходження загальних, нормальних, ермітових та η-ермітових розв’язків кватерніонових рівнянь типу Сильвестра та їх систем. Результат є важливим як з теоретичної точки зору, оскільки розвиває теорію некомутативних визначників, так із точки зору застосування у різних галузях прикладної науки, зокрема, в сингулярному системному контролі, робастному керуванні, нейронних мережах
тощо (І.І. Кирчей).

Розроблено методологію дослідження напружено-деформованого стану тонкостінних конструкцій за інтенсивних силових навантажень для оцінювання фактичних руйнівних навантажень таких конструкцій за результатами комп'ютерного моделювання. Для розв'язування сформульованої в межах геометрично нелінійної теорії термопружно-пластичності з
ізотропно-кінематичним зміцненням задачі застосовано метод скінчених елементів та розроблено відповідне програмне забезпечення. Досліджено напружено-деформований стан баків окислювачів паливного відсіку ракети за дії внутрішнього тиску та отримано оцінки їх руйнівного навантаження. Розроблені методологію, алгоритми та програмне забезпечення передано для використання в Державне підприємство «Конструкторське бюро «Південне» ім. М. К. Янгеля» (Б.Д. Дробенко) (слайд 9).

Слайд 9

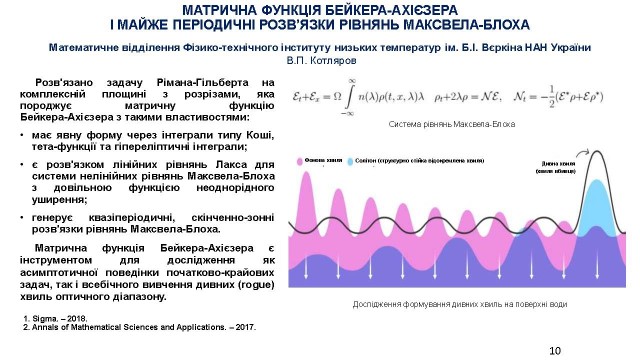
У Математичному відділенні ФТІНТ ім. Б.І Вєркіна розв'язано задачу Рімана-Гільберта на комплексній площині з розрізами, яка породжує матричну функцію Бейкера-Ахієзера з такими властивостями: вона має явне подання через інтеграли типу Коші, тета-функції та гіпереліптичні інтеграли; є розв'язком лінійних рівнянь Лакса для системи нелінійних рівнянь Максвела-Блоха з довільною функцією неоднорідного уширення; генерує квазіперіодичні, скінченно-зонні розв'язки рівнянь Максвела-Блоха. Матрична функція Бейкера-Ахієзера є інструментом для дослідження як асимптотичної поведінки початково-крайових задач, так і всебічного вивчення дивних (rogue) хвиль оптичного діапазону (В.П. Котляров) (слайд 10).

Слайд 10

Досліджено спектр оператора Максвела у періодичному середовищі з ідеальними провідними циліндричними включеннями, що мають пасткоподібний переріз. В результаті побудовано двовимірну математичну модель фотонного метаматеріалу з заданими лакунами у спектрі (акад. НАН України Є.Я. Хруслов).

Доведено гіпотезу існування фазової границі між локалізованим та делокалізованим режимами поведінки ансамблю стрічкових випадкових матриць. Ця гіпотеза є аналогом гіпотези Андерсона для дискретного оператора Лапласа, що є однією з найвідоміших невирішених проблем теорії невпорядкованих систем. Результат отримано для спрощеної кореляційної функції детермінантів стрічкових матриць на основі розробленого методу трансфер-операторів. Він є першим кроком до остаточного вирішення проблеми локальної поведінки стрічкових матриць (чл.-кор. НАН України М.В. Щербина).

Слід відзначити, що гідною оцінкою наукових здобутків вчених Відділення стало їх нагородження численними нагородами та відзнаками. Відзначу тільки деякі з них - найбільш вагомі.

Інститут прикладних проблем механіки і математики ім. Я.С. Підстригача визнано кращим у категорії «Математика» в конкурсі «Лідер науки України 2019. Web of Science Awards». Золотою медаллю та премією Наукового товариства ім. Шевченка Америки та Фонду «Україна – США» для молодих математиків відзначено роботу В.А. Марченка. Українською премією
L’ORÉAL-ЮНЕСКО «Для жінок у науці» відзначено О.О. Ванєєву. Відділення Міжнародної науково-технічної організації Інститут інженерів з електрики і електроніки (Institute of Electrical and Electronic Engineers – IEEE), яке функціонує в Інституті прикладних проблем механіки і математики
ім. Я.С. Підстригача, нагороджене преміями «Кращий IEEE Осередок 2017 року» товариства «Антени і поширення хвиль» та «Кращий IEEE Осередок 2017 року» товариства «Електронні пристрої». За участь у підготовці першого тому Великої української енциклопедії Інститут математики отримав подяку від Державної наукової установи «Енциклопедичне видавництво».

Науково-організаційна діяльність Бюро Відділення математики зосереджувалась, насамперед, на сприянні розвитку та координації фундаментальних і прикладних досліджень з актуальних напрямів математики, отриманні результатів міждисциплінарного характеру, в тому числі і при виконанні цільової програми наукових досліджень Відділення
"Розробка математичних моделей та чисельно-аналітичних методів розв’язування сучасних задач фізико-технічних і медико-біологічних наук та інформаційних технологій", яка завершилася у 2016 році, й започаткованої з 2017 року в рамках пріоритетних напрямів і тематики фундаментальних і прикладних досліджень нової цільової програми Відділення «Розробка та дослідження сучасних математичних моделей у галузі фізико-технічних та медико-біологічних наук», яка спрямована на розвиток міждисциплінарних досліджень.

Відкриття нових відомчих тем здійснювалося виключно на засадах конкурсного відбору та з урахуванням експертної оцінки фундаментальних науково-дослідних робіт Секцією математики Експертної ради з питань оцінювання тем фундаментальних науково-дослідних робіт при НАН України.

Ретельно готувалися пропозиції до бюджетного запиту Академії на кожний черговий рік та розглядалися пропозиції щодо розподілу базового бюджетного фінансування між установами відділення

Активно працювали експертні комісії з присудження премій НАН України імені видатних учених.

Постійно велася робота з контролю за діяльністю вчених рад установ щодо забезпечення високого рівня розгляду результатів виконання наукових тем та за ефективним використанням об’єктів державної власності відповідно до вимог чинного законодавства, із залучення позабюджетних коштів, добору і розстановки керівних кадрів в установах відділення, підготовки наукових кадрів вищої кваліфікації; залучення та закріплення в науковій сфері обдарованої молоді, забезпечення спадкоємності поколінь вчених; оптимізації мережі установ Відділення та структур її наукових установ. Оновлено склад та положення про Раду молодих учених при Відділенні.

У 2015 році проведено державну атестацію установ Відділення, а в установах проведено атестацію їх наукових співробітників. Аналогічна робота буде проведена у 2020 році.

Протягом звітного періоду за підсумками оцінювання діяльності Інституту математики, Інституту прикладної математики і механіки та Інституту прикладних проблем механіки і математики ім. Я.С. Підстригача їм було присвоєно категорію «А», а Центру математичного моделювання Інституту прикладних проблем механіки і математики ім. Я.С. Підстригача присвоєно категорію «Б».

На засіданнях Президії НАН України вирішено ряд питань, пов’язаних з організацією діяльності Інституту прикладної математики і механіки у зв’язку з його переміщенням з тимчасово окупованої території України до м. Слов’янськ, що дозволило зберегти його як цілісну наукову установу. Також організовано виступи з актуальних питань сьогодення на засіданнях Президії НАН України «Математичне моделювання процесів транспорту і зберігання газу»
(Я.Д. П'янило), «Математична теорія керування: нелінійна динаміка та інженерні застосування» (О.Л. Зуєв), а також виступи молодих учених.

З метою посилення зв'язків науки і освіти, інтеграції наукових напрямів з освітою при Інституті математики створено Кафедру математики Київського академічного університету НАН України та МОН України, завданням якої є підготовка співробітниками Інституту магістрів математичних спеціальностей із їх залученням до наукової роботи та з метою подальшого вступу до аспірантури Інституту. В Інституті прикладної математики і механіки відкрито дві спільні науково-дослідні лабораторії: нелінійного аналізу спільно з Донецьким національним університетом імені Василя Стуса та математичної фізики спільно з Черкаським національним університетом імені Богдана Хмельницького. Академік НАН України В.Л. Макаров протягом 2017 року був координатором Європейського проекту «Duale Ausbildung im Dialog» («Дуальна освіта в діалозі») в рамках програми «Східне партнерство», прийнятої німецьким Бундестагом, спрямованого на ознайомлення з функціонуванням дуальної системи вищої освіти в Німеччині й вивчення можливостей запровадження дуальної системи вищої освіти в Україні.

З 2017 року Українське математичне товариство поновило повноправну участь в Європейському математичному товаристві й бере участь у роботі його керівних органів та у щорічних зборах президентів європейських математичних товариств.

Велася співпраця з багатьма міжнародними науковими центрами, найбільш активно таких країн як Австрія, Бразилія, Велика Британія, Ізраїль, Італія, Канада, Китай, Кіпр, Молдова, Німеччина, Норвегія, Об'єднані Арабські Емірати, Польща, США, Франція, Чехія, Швейцарія (слайд 11).

Слайд 11

За звітний період установи Відділення були організаторами і співорганізаторами понад 100 міжнародних наукових заходів. Окрім щорічних крупних міжнародних конференцій проведено заходи, присвячені 150-річчю видатного українського математика Г. Вороного; 125-річчю від дня народження Стефана Банаха; 110-річчю від дня народження М.М. Боголюбова; 100-річчю від дня народження академіків О.В. Погорєлова, Ю.О. Митропольського, Й.І. Гіхмана, В.К. Дзядика; 95-річчю від дня народження акад. В.О. Марченка; 90-річчю від дня народження ак. Я.С. Підстригача та В.Я. Скоробогатька;
80-річчю від дня народження акад. А.М. Самойленка, чл.-кор. НАН України
Б.Й. Пташника та Б.В. Базалія.

Проведено низку урочистих заходів, присвячених 100-річчю від дня заснування Національної академії наук України, урочисто відзначено 40-річчя створення Інституту прикладних проблем механіки і математики ім. Я.С. Підстригача та 25-ліття від дня створення його Центру математичного моделювання.

Координації наукових досліджень установ Відділення та Вищих навчальних закладів сприяла активна робота наукової секції математики і математичного моделювання Західного наукового центру НАН та МОН України, яка, окрім іншого, з разом з секціями Західного наукового центру Академії розробила альтернативний Проект Закону про внесення змін до Закону України "Про наукову і науково-технічну діяльність", зареєстрований у Верховній Раді. Його окремі положення враховано у прийнятому Законі.

Вчені Відділення активно працювали в комісіях Наукового товариства ім. Шевченка з математики, механіки, інформатики та фізики, з їх ініціативи Загальні збори товариства ухвалили низку звернень до вищих органів державної влади України з приводу стану та реформування наукової і освітньої сфери у державі. Брали участь у проведенні експертиз наукових праць на здобуття премії Верховної Ради України найталановитішим молодим ученим в галузі фундаментальних і прикладних досліджень та науково-технічних робіт й експертиз наукових праць на здобуття премії Президента України.

Поглиблення міжнародної діяльності відбулося завдяки участі установ Відділення у рамковій програмі Європейського союзу з розвитку наукових досліджень та інновацій HORIZON 2020, які брали активну участь у виконанні міжнародних проектів цієї програми «Approximation Methods for Molecular Modelling and Diagnosis Tools» та «Approximation of Functions and Fourier Multipliers and their applications». З 2015 року Інститут прикладних проблем механіки і математики ім. Я.С. Підстригача разом з Київським та Львівським національними університетами забезпечує участь України як повноправного члена у міжнародному Консорціумі мережі черенковських телескопів СТА, проводячи моделювання високоенергетичних процесів у Всесвіті та відгуку на них телескопів мережі. Велися спільні дослідження з Інститутом математики Вюрцбурзького університету Юліуса Максиміліана (Німеччина), Інститутом математики Університету м. Любек (Німеччина), Математичним Інститутом Макса Планка (Німеччина) та Університетом «Політехніка ді Мілано» (Італія) та багатьма іншими. В Інституті математики відбулася заключна конференція «Математика для наук про життя» в серії заходів, які були організовані в рамках проекту HORIZON 2020 «Методи наближення методів молекулярного моделювання та діагностики». У 2020-2023 рр. в рамках HORIZON 2020 співробітники Інституту математики братимуть участь у проекті «Spectral Optimization: From Mathematics to Physics and Advanced Technology».

Зростає присутність наукових праць та видань установ Відділення математики у міжнародних базах даних та системах цитування наукової літератури завдяки збільшенню кількості публікацій вчених у зарубіжних виданнях, їх входженню до складу редакційних рад англомовних видань.

Бюро Відділення та установи Відділення багато уваги приділяли популяризації математики. Щороку в рамках Всеукраїнського фестивалю науки проводилися різноманітні заходи для школярів та студентів, організовувалися зустрічі вчених Академії з учнями МАН, молоді вчені керували науковими дослідженнями школярів. Вчені Відділення брали участь у проведенні як всеукраїнських, так і міжнародних олімпіад юних математиків, готували до них школярів, читали науково-популярні лекції в рамках літньої школи МАН, проводили різноманітні наукові свята, «ФізМатДень», «Жінки в математиці: історія та перспективи», Київський математичний фестиваль, літні математичні школи для учнів Харківського ліцею, всеукраїнський турнір математичних боїв «Харків мастерс», семінар з підвищення кваліфікації для вчителів математики, проводився запис відеолекцій з курсів математики. Установи Відділення подавали свої пропозиції до Міністерства освіти і науки України щодо забезпечення належного рівняння викладання математики і школах, атестації наукових кадрів, рецензували підручники та посібники. Готувалися публікації, вчені регулярно давали інтерв’ю та коментарі ЗМІ, виступали на радіо та телебаченні.

Звіт у форматі PDF

Презентація до звіту у форматі PDF